Artificial mental model
Following Minsky’s mental model of general purposes50 as a general guide, Fig. 1 shows an approach of an artificial mental model for the passenger agent, composed of three levels—Reactive, Deliberative, and Reflective—and two layers—Executive and Memory.
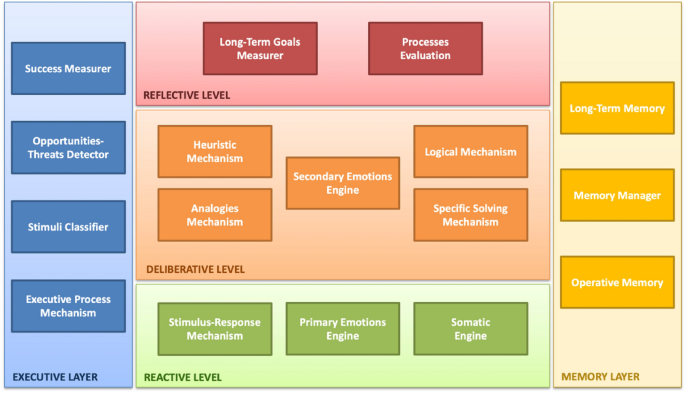
Artificial mental model (source: own elaboration).
Reactive Level: This level represents the first level of response to internal and external stimuli. The “Stimulus–Response Mechanism” is directly associated with actions such as “If … then Do.” Additionally, the component “Primary Emotions Engine” controls the valuation and status of the entity’s primary emotions.
Deliberative Level: This level addresses stimuli and situations that require more sophisticated responses. Its components are as follows:
-
Analogies Mechanism This component looks for analogies between the current problem or situation and past successful mechanisms used for problem-solving and decision-making.
-
Heuristic Mechanism This component allows the use of ad hoc methods or experience-based methods to address specific situations.
-
Logical Mechanism This component applies logical rules to problem-solving and decision-making.
-
Specific Solving Mechanism This component represents all procedures the entity employs to deal with situations and respond to stimuli that cannot be classified under the above components.
-
Secondary Emotions Engine This component combines knowledge, experience, feelings, primary emotions, and somatic reactions.
Reflective Level: This level enables the entity to think and reflect on its decision-making processes and the accomplishment of its goals. In addition, it is possible to reflect on how its internal processes are performed, including the use of heuristics, logical procedures, and analogies mechanism.
Executive Layer: This layer has mechanisms to classify stimuli based on their origin, level of intensity, duration, etc. It also identifies opportunities and threats in the environment that may affect goal achievement, and measures success in decision-making. The component called “Executive Process Mechanism” is enabled to control and monitor the implementation of each decision.
Memory Layer: This layer includes the “Memory Manager” component, which is responsible for storing and retrieving information required for the current action (Operative Memory) as well as information related to past events, situations, and decisions (Long-Term Memory).
Mathematical formulation
This work considers a simulated artificial city comprising four types of streets: normal, unsafe, congested, and tourist. For the purposes of this research work, the travel time corresponds to the simple sum of the required transit time for each of the streets that make up a travel route:
$$time_{t} = \mathop \sum \limits_{i = 1}^{n} nStreet_{i,t} \cdot nt + \mathop \sum \limits_{j = 1}^{u} uStreet_{j,t} \cdot ut + \mathop \sum \limits_{k = 1}^{c} cStreet_{k,t} \cdot ct + \mathop \sum \limits_{l = 1}^{t} tStreet_{l,t} \cdot tt,$$
(1)
where nStreeti,t, uStreetj,t, cStreetk,t, and tStreetl,t represent the trip made from street i in iteration t, corresponding to a normal, unsafe, congested, and tourist street, respectively. On the other hand, the parameters nt, ut, ct, and tt, represent the time factors of a normal, unsafe, congested, and tourist street, respectively.
The travel distance corresponds to the simple sum of the required transit distance for each of the streets that make up a travel route:
$$distance_{t} = \mathop \sum \limits_{i = 1}^{n} nStreet_{i,t} \cdot nd + \mathop \sum \limits_{j = 1}^{u} uStreet_{j,t} \cdot ud + \mathop \sum \limits_{k = 1}^{c} cStreet_{k,t} \cdot cd + \mathop \sum \limits_{l = 1}^{t} tStreet_{l,t} \cdot td$$
(2)
where the parameters nd, ud, cd, and td, represent the distance factors of a normal, unsafe, congested, and tourist street, respectively, similar to the definition of Eq. (1), considering the factor of distance instead of time.
On the other hand, the cost of travel is determined according to Eq. (3):
$$cost_{t} = veCost_{t} \cdot vtf + time_{t} \cdot tfc + distance_{t} \cdot dfc,$$
(3)
where veCostt corresponds to the operational cost associated with a specific type of vehicle (e.g., city car, luxury car) considered in the trip t; timet corresponds to the travel time of the trip t calculated according to Eq. (1); distancet corresponds to the route distance from an origin point to a destination point in the trip t defined in Eq. (2). Parameters vtf, tfc, and dfc correspond to the cost impact of a specific vehicle-type choice, the cost associated with the time spent in transportation, and the cost per unit of distance traveled, respectively.
Meanwhile, the utility derived from travel is determined according to Eq. (4):
$$utility_{t} = \mathop \sum \limits_{i = 1}^{n} nStreet_{i,t} \cdot nu + \mathop \sum \limits_{j = 1}^{u} uStreet_{j,t} \cdot uu + \mathop \sum \limits_{k = 1}^{c} cStreet_{k,t} \cdot cu + \mathop \sum \limits_{l = 1}^{t} tStreet_{l,t} \cdot tu,$$
(4)
where nu, uu, cu, and tu represent the utility factor of a normal, unsafe, congested, and tourist street, respectively, which is the utility derived from traveling a block of this type of street. It is worth mentioning that utility is conceived as a subjective measure of each passenger agent that influences the decision-making process of which type of service to use and tries to be a simile of the way in which human beings make their decisions, based on their experience and stimuli.
When a passenger agent sends a trip request, they may receive several travel proposals, which are evaluated independently by calculating a score, as shown in Eq. (5):
$$score_{to,t} = time_{to,t} \cdot ti + cost_{to,t} \cdot ci + utility_{to,t} \cdot ui + somaticIndex_{to,t} \cdot sii$$
(5)
where scoreto,t represents the score associated with the travel proposal received from the transport operator to in the trip t; furthermore, somaticIndexto,t, corresponds to an index proposed in this research that links the somatic reaction derived from the transport experience with the quantification of that experience. In this case, ti, ci, ui, and sii correspond to parameters representing the weight of time, cost, utility level, and somatic index, respectively.
Concerning the somaticIndex variable, a positive value represents a good level of travel experiences of a passenger with the transport operator to. Conversely, a negative value represents a poor level of travel experiences of a passenger with the transport operator to. It is important to mention that for each passenger-transport operator relationship, there is an independent somaticIndex variable that represents said relationship. Likewise, the initial somaticIndex value is zero (i.e., a neutral value) and varies over time according to how the passenger evaluates the travel experience derived from transport operator service.
As mentioned in previous sections, this work suggests the incorporation of a somatic index as a mechanism for evaluating and registering the passenger travel experience associated with different transport operators. Particularly, the somaticReaction variable allows determining the intensity of the reaction experienced by the passenger after being notified that it is necessary to replan (in real-time) the travel to the destination point. In this sense, somaticReaction is calculated according to Eq. (6):
$$somaticReaction_{tot} = \tan^{ – 1} \left[ {\Delta time_{tot} \cdot itv + \Delta cost_{tot} \cdot icv + \Delta utility_{tot} \cdot iuv} \right] \pm rand\left[ { – 0.5 , 0.5} \right] \cdot irf$$
(6)
where Δtimeto, Δcostto, and Δutilityto correspond to the variation between the original travel and the updated travel time, cost, and utility, respectively, associated with the travel proposal received from the transport operator to in the trip t. On the other hand, the parameters itv, icv, iuv, and irf represent the weight of time, cost, utility, and random effect, respectively. For this research, the random effect is uniformly distributed between [− 0.5, 0.5], a value that can be modified according to the specific requirement of the application.
The calculation of the somaticReaction variable suggests the use of a smoothing function with the idea of smoothing extreme values (of very high positive intensity or very low negative intensity), such as a logistic, sigmoid, or arctangent function, among others. For this research, the arctangent function was used for calculation simplicity. However, it can be replaced by a more general function depending on the application. Likewise, the incorporation of a random value allows granting a degree of flexibility in the somaticReaction value, understanding that exposure of a person to the same stimulus (or result) over time does not guarantee the same somatic reaction. It should be noted that the Somatic reaction is associated with the transport operator to.
Below we show the example of somatic reaction behavior for synthetic data in Fig. 2. In this graph, we can see that as the values become more extreme, the value of the reaction tends to stabilize, which allows us to control the overall agent behavior. In addition, confidence bands are shown which correspond to the randomness effect described in Eq. (6).
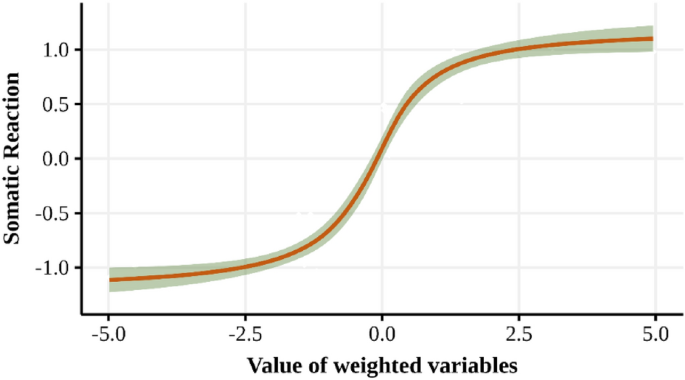
Example of somatic reaction behavior [source: own elaboration].
The somaticIndex is defined according to Eq. (7):
$$somaticIndex_{to} = siw \cdot somaticIndex_{to} + \left( {1 – siw} \right) \cdot somaticReaction_{tot}$$
(7)
where somaticIndexto initially in zero, registers the passenger’s experience regarding the service of a transport operator to and siw corresponds to the weight of the previous somatic index in the modeling. Somatic index modeling is characterized by an autoregressive effect, in other words, the effect of the previous somatic index affects the observed value of the current somatic index. The modeling proposed in this initial work considers an equivalent weight between the value of the previous somatic index and the somatic reaction, which allows us to conceptualize a memory of the artificial agent about its previous experiences.
Regarding the somaticIndexto valuation, this research considers assigning an equivalent connotation both to the memory of the “passenger agent—transport operator” relationship and the most recent reaction experienced by the passenger agent prior to the service received from transport operator to. In relation to the somatic marker hypothesis, this last experienced reaction by the passenger agent can be associated with a “somatic reward” or a “somatic punishment,” which correspond to positive or negative sensations that may linger in the working memory of the autonomous agent47. These sensations can emulate a sense of well-being, regret, or discomfort, and they influence the decision-making process. In the case of this work, the somaticReaction variable acts as an artificial somatic reward or punishment based on the assessment derived from the most recent experience.
Algorithm 1 describes the general trip request process of a passenger agent. All the steps contained in the algorithm are associated with the passenger agent. The algorithm begins with the definition of the trip’s origin and the destination points. The passenger agent then submits their request. The algorithm utilizes the route determination algorithm designed and presented by51. Upon receiving travel proposals, the passenger agent calculates the travel time, distance, cost, and utility for each route. Each travel proposal is assigned a score, and the proposals with the highest score are chosen. The passenger agent then activates the service provision with the corresponding transport operator. Subsequently, the passenger agent receives route information, where if said information corresponds to a replanning notification, the agent obtains the new route to follow. From this new route, the passenger agent recalculates the travel metrics, which comprise the travel time, distance, cost, and utility derived from the route. Once the travel metrics have been updated, the passenger agent experiences an artificial somatic reaction, which, in turn, affects the update of the somaticIndex, generating a record in the working memory for the next decision and a record in the long-term memory.

Algorithm 1. General trip request process of a passenger agent.
Regarding algorithm 1 and the artificial mental model presented in Fig. 1, steps 1, 2, and 4 are associated with an executive process mechanism (within the executive layer). Meanwhile, steps 3 and 6 are associated with the memory layer, specifically, the operative memory (of the passenger agent). On the other hand, steps 7–11 are specific solving mechanisms since they correspond to mechanisms for calculating travel metrics. Both the travel proposal and its score are recorded in the working memory. Meanwhile, steps 14–17 are associated with the deliberative level since they allow the passenger agent to decide on the transport operator and operationalize said decision. In addition, faced with a real-time route replanning (logical evaluation of step 18 of the algorithm), steps 19–23 associated with calculating travel metrics are performed (that is, at a deliberative level).
The primary effect derived from the route change corresponds to the somatic reaction experienced by the passenger agent and is obtained in step 24 (at the reactive level of the artificial mental model, through the Somatic Engine component). Meanwhile, the subsequent effect of this somatic reaction is obtained in step 25 (at the deliberative level of the artificial mental model, through the Secondary Emotions Engine component), and is reflected by using an index (at the level of secondary emotions) representing the passenger’s experience with the service received from a specific transport operator.